Dividing Fractions

Many adults remember that when dividing by a fractions, you invert and multiply. But do you know why?

Visualizing Division

First let's look at what it means to divide using whole numbers.

If we have a problem 6 ÷ 3, we can ask: How many 3s are there in 6?

Here are our six things:

Find and circle 3 of them

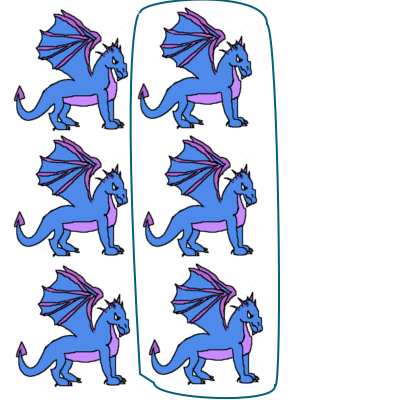
six dragons with a circle around 3 of them

then repeat until we run out of things.

We have 2 groups, so the answer is 2.

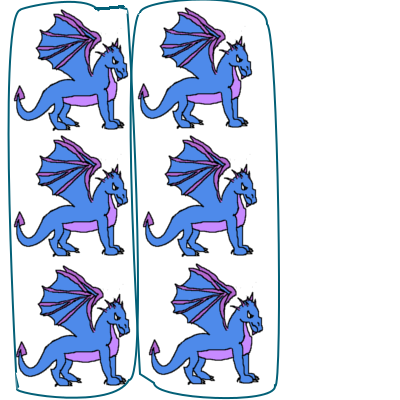
Now, with ducks, let's look at another question. 8 ÷ 4 can be the question: If we divide 8 into 4 groups, how many are in each group?

Here are the ducks eight yellow cartoon ducks

and here are four boxes to put them in 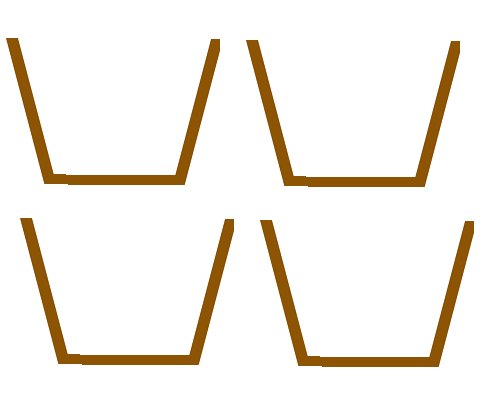four brown outlines to represent boxes .

We want even groups, so put one in each box. 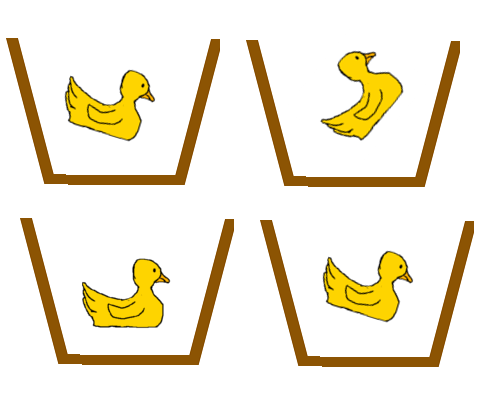then repeat until we run out. 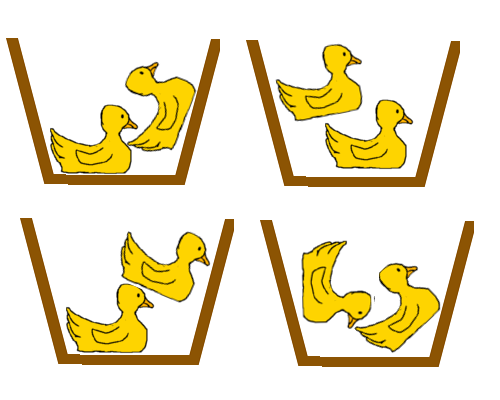Since the groups are the same, and no ducks are left over, our answer is the number of ducks in each box: 2.

Now with Fractions

If we have 3 ÷ 1/5, we can ask How many 1/5s in 3? Or If we divide 3 into 1/5 groups, how many in each group?

Let's start with the first question. How many 1/5s in 3? Here are our 3 things: three black circles We are looking for 1/5s, so cut each into 5 pieces. 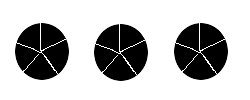3 black circles cut into 5 wedges each Each circle has 5 pieces, and there are 3 circles, so there are 3x5= 15 pieces. Because 1 has 5 1/5s in it, dividing by 1/5 becomes multiplying by 5. And so 3 ÷ 1/5 = 3 x 5 = 15.

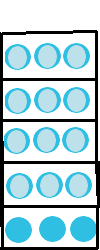We can instead ask: If we divide 3 into 1/5 groups, how many in each group? What is "1/5 groups"? Well, it means the three circles will be 1/5 of a larger group. Here are 3 things: three small blue circles Now imagine that they are only 1/5 of something larger: three small blue circles in a black rectangle, with four more rectangles above. Here are the rest of the group: five rectangles connected vertically, with 3 blue circles in the lowest, 3 lighter blue in each other To go from 1/5 of the group, to the whole group, multiply by 5 to get 15.