Visualizing Positive and Negative Numbers

When we first learn about numbers they are usually positve. We count objects. And using objects can help find answers to arithmetic problems. We develop intuition about how numbers work. But negative numbers can be harder to understand. We learn rules like "two negatives make a positive" but aren't sure when to apply them.

Here are 3 ways to think about how positive and negative numbers interact.

1. Think money, postive is earning, negative is debt.

   This helps a lot of people. If you are adding a negative numbers, it's a new debt you owe. If you subtract a negative, the debt has been forgiven or paid off.

2. Number line movement

For some people, a numberline (with or without a duck) helps them think about negative numbers. Read about adding and subtracting on a numberline

3. 2-sided counters.

   This is the way we are going to look at now.

Negative numbers with Counters

With 2-sided counters, one side is postive the other negative. You can make them by gluing 2 colors of paper together or coloring one side of your counters. The counters in these pictures are the units from an old set of algebra tiles. I use off-white as positive and red as negative. If you have one of each, you have zero total value. Here's a picture of zero:

There are multiple ways of showing any given number, depending on how many extra zeros you add. What number do each of these represent? (click to reveal the answer)

-1

2

-5

Add a postive plus a negative

Let's look at 4 + -2 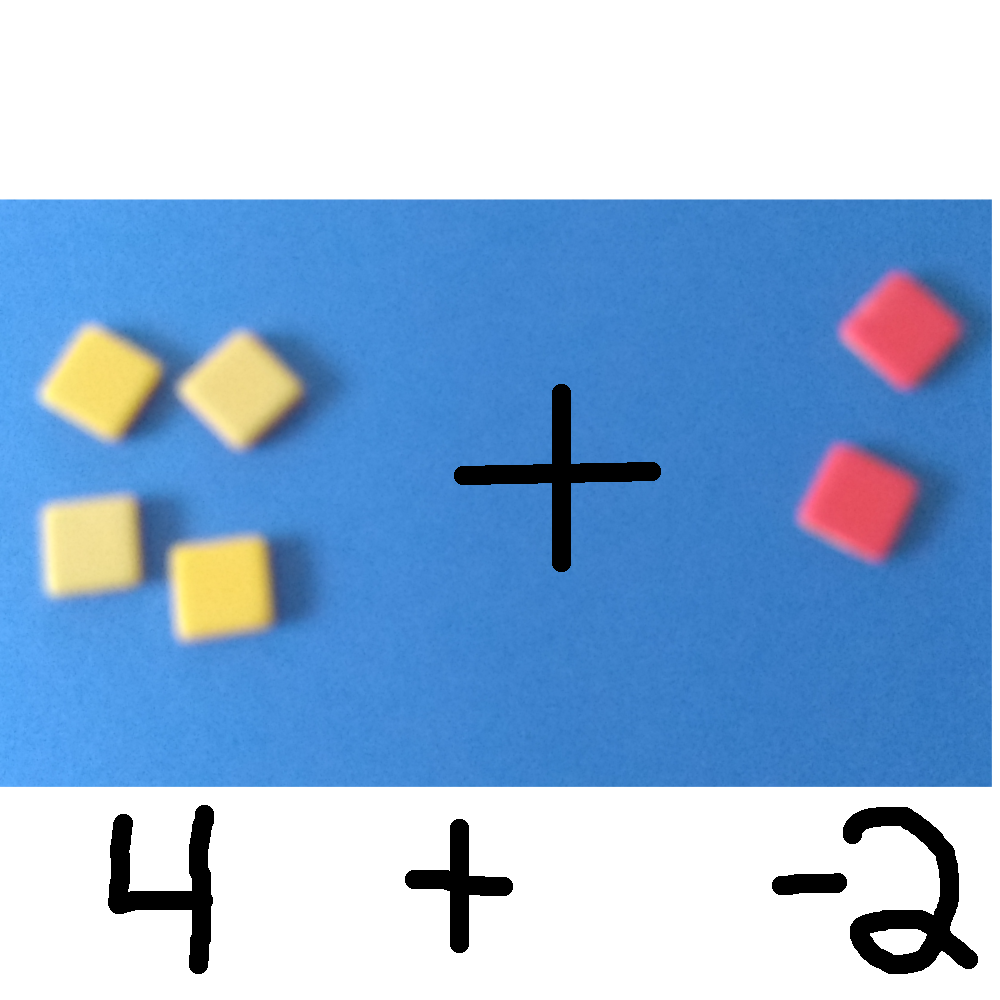Now collect pairs that make zero and now remove the zeros and we see that 4 + -2 = 2.

Subtraction

Subtraction is taking away. So 5-2 means we start with 5 and take 2 away leaving 3.

If we want to take away a negative number, we need some red counters to remove. So 5 -(-2) starts with 5 again then we add some zeros (it's still worth 5) and now we take away -2 leaving 7 positive counters, 5 - (-2) = 7.